개발자입니다
[클린코드 파이썬] 13장: 빅오를 활용한 알고리즘 성능 분석과 개선 본문
timeit 모듈
소프트웨어 개발 분야에서 "섣부른 최적화는 만악의 근원"이라는 말이 있다.
다음과 같이 반복가능 언패킹이라고 불리는 다중 할당 기법을 사용해 두 변수를 교환할 수 있는데 짧은 시간 안에 실행된다.
import timeit
timeit.timeit('a, b = 42, 101; a, b b = b, a')
# 0.053624899999931586
timeit.timeit() 함수는 두 번째 문자열 인수로 설정코드를 취할 수도 있다. 설정 코드는 첫 번째 코드 문자열을 실행하기에 앞서 한 번만 실행된다. 또한 number 키워드 인수에 대한 정수를 전달해 기본 시행 횟수를 변경할 수도 있다.
기본적으로 timeit.timeit()으로 넘기는 코드 문자열은 다음과 같이 프로그램의 다른 변수와 함수에 접근할 수 없다.
import timeit
spam = 'hello'
timeit.timeit('print(spam)', number=1) # spam 출력을 측정한다
# Traceback (most recent call last):
# File "D:\git\jongkwangyun.github.io\cleanCodePython\test.py", line 4, in <module>
# timeit.timeit('print(spam)', number=1) # spam 출력을 측정한다
# File "C:\Program Files\Python\Python310\lib\timeit.py", line 234, in timeit
# return Timer(stmt, setup, timer, globals).timeit(number)
# File "C:\Program Files\Python\Python310\lib\timeit.py", line 178, in timeit
# timing = self.inner(it, self.timer)
# File "<timeit-src>", line 6, in inner
# NameError: name 'spam' is not defined이 문제를 수정하려면 globals 키워드 인수에 대해 globals() 반환 값을 함수에 전달한다.
import timeit
spam = 'hello'
timeit.timeit('print(spam)', number=1, globals=globals())
# hello
# 1.4800000030845695e-05
cProfile 프로파일러
작은 코드 조각을 측정하는 데는 timeit 모듈이 유용하지만, 전체 함수나 프로그램을 분석하는 데는 cProfile 모듈이 더 효과적이다. 프로파일링은 프로그램의 속도, 메모리 사용 등의 여러 측면을 체계적으로 분석한다.
cProfile 프로파일러를 사용하려면 측정하려는 코드 문자열을 cProfile.run() 함수에 전달해야 한다.
import time, cProfile
def addUpNumbers():
total = 0
for i in range(1, 1000001):
total += i
cProfile.run('addUpNumbers()')이 프로그램 실행하면, 출력은 다음처럼 보일 것이다.
4 function calls in 0.065 seconds
Ordered by: standard name
ncalls tottime percall cumtime percall filename:lineno(function)
1 0.000 0.000 0.065 0.065 <string>:1(<module>)
1 0.065 0.065 0.065 0.065 test.py:2(addUpNumbers)
1 0.000 0.000 0.065 0.065 {built-in method builtins.exec}
1 0.000 0.000 0.000 0.000 {method 'disable' of '_lsprof.Profiler' objects}각 행은 다양한 함수와 해당 함수에서 소비된 시간을 나타낸다. 출력 결과에 나오는 열의 설명은 다음과 같다.
ncalls: 이 함수가 호출된 횟수
tottime: 이 함수에서 호출한 다른 함수들의 시간을 제외하고 이 함수 자체에서 소비된 총 시간
percall: 총 호출 시간을 누적 호출 횟수로 나눈 값
cumtime: 이 함수와 이 함수가 호출한 모든 다른 함수들에 소비된 누적 시간
filename:lineno(function): 함수가 들어있는 파일과 행 번호
구성 요소 중 하나를 개선하면 전체 프로그램이 얼마나 빨라지는지를 계산하는 공식인 암달의 법칙amdahl's Law가 있다. 정확한 공식은 전체 작업 속도 향상 = 1 / ((1 - p) + (p / s))인데, 여기서 s는 구성 요소에 대한 속도 증가이고 p는 전체 프로그램의 해당 구성 요소에 대한 부분값이다. 따라서 프로그램 전체 실행시간의 90%를 차지하는 구성 요소의 속도를 2배로 하면 1 / ((1 - 0.9) + (0.9 / 2) = 1.818, 즉 전체 프로그램의 82%에 해당하는 속도 향상을 얻을 수 있다. 이런 향상은 전체 실행시간의 25%만을 차지하는 부분의 속도를 3배로 뻥튀기해 봤자 1 / ((1 - 0.25) + (0.25 / 2) = 1.143, 전체 속도 상승이 14% 수준 정도인 상황보다는 낫다.
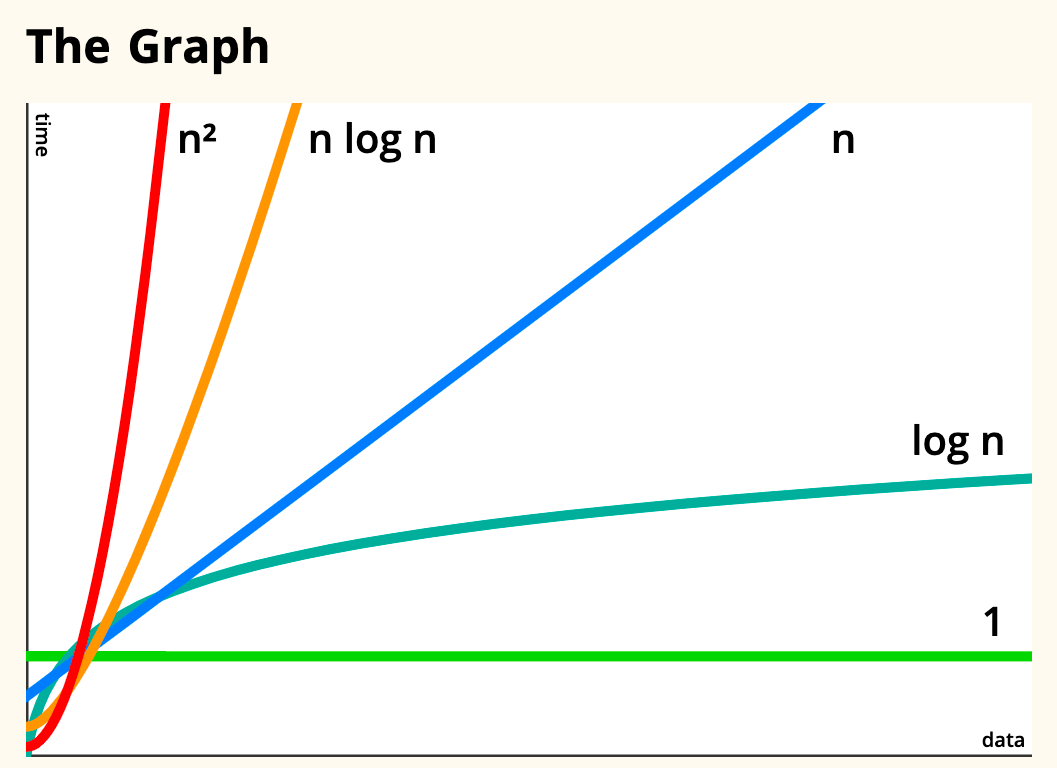
빅오 알고리즘 분석
빅오Big O란 코드가 어떻게 확장될 것인지를 설명하는 알고리즘 분석의 한 형태다.
빅오 차수
- O(1), 상수 시간(가장 낮은 차수)
- O(log n), 로그 시간
- O(n), 선형 시간
- O(n log n), 선형로그 시간
- O(n²), 다항 시간
- O(2ⁿ), 지수 시간
- O(n!), 팩토리얼 시간(가장 높은 차수)
빅오는 소괄호 ( ) 한 쌍 안에 수식으로 차수를 기입하고 대문자 O 뒤에 붙이는 방식으로 표기한다. 대문자 O는 차수order 또는 대략의 차수on the order of를 나타내며, n은 코드가 작업할 입력 데이터의 크기를 나타낸다. 우리는 O(n)을 big oh n 또는 big oh of n이라고 표기하고 '빅오 엔'이라고 읽는다.
간략히 정리하자면 다음과 같다.
- O(1)과 O(log n) 알고리즘은 빠르다.
- O(n)과 O(n log n) 알고리즘은 나쁘지 않은 편이다.
- O(n²), O(n!), O(2ⁿ) 알고리즘은 느리다.
최악의 시나리오를 측정하는 빅오
빅오는 어떤 작업에서도 최악의 시나리오를 콕 찍어서 측정한다.
코드의 빅오 차수를 파악해보자
코드의 빅오 차수를 알아내기 위해서는 네 가지 작업을 해야 한다.
- n이 무엇인지 확인
- 코드 단계 세기
- 낮은 차수 무시
- 계수 생략
예를 들어 다음과 같은 readingList() 함수의 빅오를 찾아보자.
def readingList(books):
print('Here are the books I will read:')
numberOfBooks = 0
for book in books:
print(book)
numberOfBooks += 1
print(numberOfBooks, 'books total.')n은 코드가 작업할 입력 데이터의 크기를 나타낸다. 함수에서 n은 거의 항상 파라미터를 기반으로 한다. readingList() 함수의 유일한 파라미터는 books이기 때문에, books의 크기로는 n이 적합해 보인다.
이 코드의 단계를 세어 보자. 한 코드 행을 한 단계라고 생각하면 된다.
def readingList(books):
print('Here are the books I will read:') # 1단계
numberOfBooks = 0 # 1단계
for book in books: # n * (루프문 안의 단계 수)
print(book) # 1단계
numberOfBooks += 1 # 1단계
print(numberOfBooks, 'books total.') # 1단계for 루프문 행을 제외한 각 코드 행을 한 단계로 취급한다. 루프문 내부에 2단계가 있기 때문에 총 2 × n단계다. 따라서 단계 횟수는 다음과 같다.
def readingList(books):
print('Here are the books I will read:') # 1단계
numberOfBooks = 0 # 1단계
for book in books: # n * 2단계
print(book) # (이미 계산됨)
numberOfBooks += 1 # (이미 계산됨)
print(numberOfBooks, 'books total.') # 1단계이제 총 단계 수를 계산하면 1 + 1 + (n × 2) + 1가 된다. 이 표현식을 간단히 다시 정리해서 2n + 3라고 쓴다.
빅오는 세부사항을 나타내지 않으며, 일반적인 지표일 뿐이다. 따라서 계산에서 더 낮은 차수들은 생략한다. 더 낮은 차수를 생략하면 2n만 남는다.
다음은 차수에서 계수를 생략한다. 2n의 계수는 2이므로, 계수를 생략하고 나면 n이 남는다. 결과적으로 readingList() 함수의 최종 빅오 값은 O(n), 즉 선형 복잡도라는 사실을 알 수 있다.
빅오 분석 예제
def countBookPoints(books):
points = 0 # 1단계
for book in books: # n * (루프문 단의 단계 수)
points += 1 # 1단계
for book in books: # n * (루프문 안의 단계 수)
if 'by Al Sweigart' in book: # 1단계
points += 1 # 1단계
return points # 1단계단계 수는 1 + (n × 1) + (n × 2) + 1가 되며, 동일 항들을 더하면 3n + 2가 된다. 최종적으로 O(n), 즉 선형 복잡도가 된다.
def iLoveBooks(books):
for i in range(10): # 10 * (루프문 안의 단계 수)
print('I LOVE BOOKS!!!') # 1단계
print('BOOKS ARE GREAT!!!') # 1단계이 함수에는 for 루프문이 있지만, books 리스트를 반복하지 않으며, books의 크기에 무관하게 20단계를 수행한다. 이를 20(1)로 다시 쓸 수 있다. 여기서 계수 20을 생략하면 O(1), 즉 상수 시간 복잡도가 된다.
def finalDuplicateBooks(books):
for i in range(len(books)): # n단계
for j in range(i + 1, len(books)): # n단계
if books[i] == books[j]: # 1단계
print('Duplicate:', books[i]) # 1단계for i 루프문 내부에서 for j 루프문을 수행한다. n² 연산을 수행한다. O(n²) 다항시간 연산이 된다.
한눈에 분석하는 빅오
일반적인 규칙 몇 가지를 살펴보자.
- 코드가 데이터에 전혀 접근하지 않으면 O(1)이다.
- 루프문에서 데이터에 접근하면 O(n)이다.
- 두 중첩된 루프문에서 데이터를 순회하면 O(n²)이다.
- 함수 호출은 한 단계로 세지 않고 함수 내부 코드의 총 단계 수를 센다.
- 코드가 데이터를 반복적으로 반으로 나누는 분할 정복 단계로 구성되어 있다면 O(log n)이다.
- 코드가 데이터에서 아이템당 한 번씩 이루어지는 분할 정복 단계로 구성되어 있다면 O(n log n)이다.
'Python > 클린 코드, 이제는 파이썬이다' 카테고리의 다른 글
| [클린 코드 파이썬] 14장: 실전 프로젝트: 하노이 탑과 사목 게임 (2) | 2024.09.14 |
|---|---|
| [클린코드 파이썬] 11장: 주석과 타입 힌트 (2) | 2024.09.04 |
| [클린코드 파이썬] 10장: 파이썬다운 함수 만들기 (0) | 2024.09.03 |
| [클린코드 파이썬] 8장: 파이썬에서 빠지기 쉬운 함정들 (0) | 2024.09.02 |
| [클린코드 파이썬] 6장: 파이썬다운 코드를 작성하는 법 (5) | 2024.09.01 |
